I was amazed when I read in Playing At the World about De Vetula, the 13th-century poem that addressed the most important problem of science: how likely are you to roll an 18 STR?
 De Vetula is a real poem, and amidst the gambling adventures of its protagonist, it really has probability calculations for 3d6. I love that the world’s first accurate discussion of probability is so directly applicable to D&D. This plus the Roman d20 almost makes you think that there’s been a secret society of D&D players throughout history (the Brontes were probably members).
De Vetula is a real poem, and amidst the gambling adventures of its protagonist, it really has probability calculations for 3d6. I love that the world’s first accurate discussion of probability is so directly applicable to D&D. This plus the Roman d20 almost makes you think that there’s been a secret society of D&D players throughout history (the Brontes were probably members).
I decided I’d track down the relevant section of the poem. Here’s a page of the manuscript:
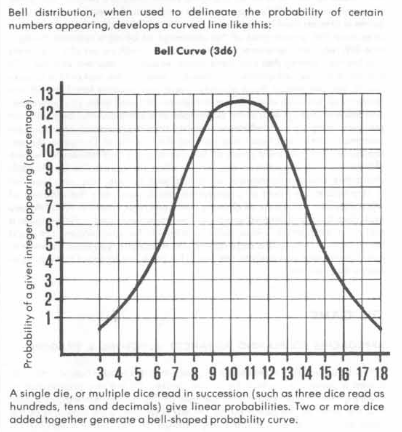
That’s a bell curve there, and along the right side, you see the familiar 3-18 range familiar to D&D players. This doesn’t look much like a medieval poem. What it looks a lot like is the beginning of the 1e Dungeon Master’s Guide:
In case it’s of interest to D&D players or people interested in probability, here’s Nancy Prior’s translation of the relevant section of the poem:
Perhaps, however, you will say that certain numbers are better
Than others which players use, for the reason that,
Since a die has six sides and six single numbers,
On three dice there are eighteen,
Of which only three can be on top of the dice.
These vary in different ways and from them,
Sixteen compound numbers are produced. They are not, however,
Of equal value, since the larger and the smaller of them
Come rarely and the middle ones frequently,
And the rest, the closer they are to the middle ones,
The better they are and more frequently they come.
These, when they occur, have only one configuration of pips on the dice,
Those have six, and the remaining ones have configurations midway between the two,
Such that there are two larger numbers and just as many smaller ones,
And these have one configuration. The two which follow,
The one larger, the other smaller, have two configurations of pips on the dice apiece.
Again, after them they have three apiece, then four apiece.
And five apiece, as they follow them in succession approaching
The four middle numbers which have six configurations of pips on the dice apiece.
The small table set out below will make these things easier for you:18 666
17 665
16 664 655
15 663 654 555
14 662 653 644 554
13 661 652 643 553 445
12 651 642 633 552 543 444
11 641 632 551 542 533 443
10 631 622 541 532 442 433
9 621 531 522 441 432 333
8 611 521 431 422 332
7 511 421 331 223
6 411 322 222
5 311 221
4 211
3 111These are the fifty-six ways for the numbers to fall,
And the number of them can neither be smaller nor larger.
For when the three numbers which make up the throw are alike,
Since six numbers can be matched up with one another,
There are also six configurations of pips on the dice, one for any number.
But, when one of them is not like the others,
And two are the same, the configurations of pips on the dice can vary in thirty ways,
Because, if you duplicate any of the six numbers,
After you have added any of the numbers which remain, then
You will come up with thirty, as if you multiply six five-fold.
But, if all three numbers are different,
Then you will count twenty configurations of pips on the dice
For this reason: Three numbers can be successive
In four ways and non-successive in just as many, but
If two are successive and a third non-successive,
The figure set out below for your perusal makes this clear:
You will discover from the one side twice three ways and from the other thrice two ways.666 555 444 333 222 111 665
664 663 662 661 556 554 553
552 551 446 445 443 442 441
336 335 334 332 331 226 225
224 223 221 116 115 114 113
112 654 543 432 321 642 641
631 531 653 652 651 621 521
421 542 541 643 431 632 532Again, if one looks more closely into the configurations of pips on the dice,
There are some which have only one way of falling,
And there are others which have three or six, since the ways of falling
Cannot be different when the three numbers in question
Are the same. But, if one of them should be unlike,
And two the same, three ways of falling emerge
After a different number turns up on top of any of the dice.
But if they are all unlike, you will discover
That they can vary in six ways, since,
When you give any position to one of the three, the remaining two change places,
Just as an alternation of the configuration of pips shows. And so
They vary in fifty-six ways in the configurations of pips on the dice,
And the configurations in two hundred and sixteen ways of falling.
When these have been divided among the compound numbers which players use,
Just as they must be distributed among them,
You will learn full well how great a gain or a loss
Any one of them is able to be.
The table written out below can make this clear to you:How many configurations of pips on the dice and ways of falling any compound number would have
3 18 configurations of pips on the dice 1 way of falling 1 4 17 configurations of pips on the dice 1 way of falling 3 5 16 configurations of pips on the dice 2 way of falling 6 6 15 configurations of pips on the dice 3 way of falling 10 7 14 configurations of pips on the dice 4 way of falling 15 8 13 configurations of pips on the dice 5 way of falling 21 9 12 configurations of pips on the dice 6 way of falling 25 10 11 configurations of pips on the dice 6 way of falling 27
Thanks to Jon Peterson for letting me know that this poem existed!







Fantastic!
What’s funny about this is that, as a professional medievalist, I know of De Vetula for completely different reasons.
very useful for the chinese game of Sic Bo